Plane Stress

Introduction

Analyzing solid mechanics problems can be challenging, to reduce the complexity we often try to isolate parts, find symmetry in the shape or in the load.

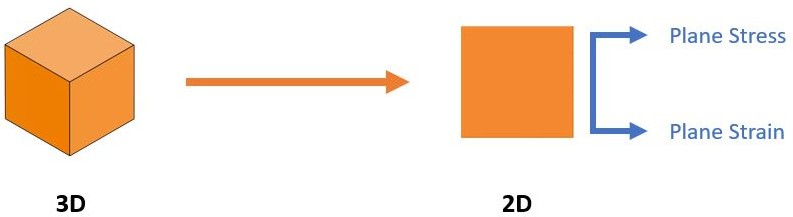
In specific cases we can change the 3D problem to a 2D problem, and this will be a very important simplification for us, considering that hand calculation validation process will be much easier on a 2D analysis.

General Stress

General stress

Forces acting at the surfaces of solids generate internal forces, described as STRESS. There are two types of stress that a structure can experience:

1. Normal Stress: When a force acts perpendicular to the surface of an object it exerts a normal stress σ
2. Shear Stress: When a force acts parallel to the surface of an object, it exerts a shear stress τ

For solid mechanics we will use the tensor or matrix of stress representing the 9 types of stress a solid can sustain when a force is applied to the surface :

The unit of stress is the Pascal (Pa): 1Pa is equivalent to a force of 1 Newton acting over an area of 1 metre squared. Typical units used in engineering applications are the kilopascal, megapascal, and the gigapascal.

Normal Stress

The solid is subjected to tension by opposite forces of magnitude F along its axis. If the system is in equilibrium. The stress throughout the bar, across any horizontal surface, can be expressed simply by the single number σ, calculated simply with the magnitude of those forces, F, and cross sectional area A :

Shear Stress

Consider now the case of shear forces, that is, forces which act tangentially to surfaces. A normal force F acts on a block. he block does not move and, to maintain equilibrium, the force is resisted by a friction force.

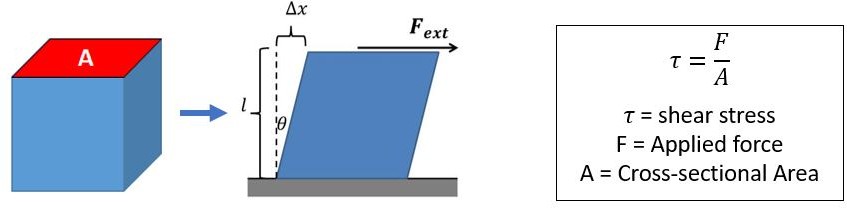
Assuming a uniform distribution of load, the stress in this case is called shear stress.

Plane Stress

Equilibrium

In structural mechanics we are using the equilibrium principle to analyze stress and strain inside the solid :

Plane stress

The state of plane stress is defined as follows:

Plane Stress:

If the stress state at a material particle is such that the only non-zero stress components act in one plane only, the particle is said to be in plane stress.

Plane stress assumes that the three stress tensor components relating to one direction are zero.

This is great for analyzing very thin plates that are loaded only in the plane, but it can also be applied to the surface of thicker components. In fact, the surface of a plate is the only location where true plane stress conditions can exist. It is a perfect representation of the boundary condition.

 

Let’s say that the three stress tensor components relating to Z direction are zero :

Plane Stress Static Structural

Johan Ravail October 21, 2021